To calibrate venturi meter by establishing the relationship between flow rate and pressure difference and to find its coefficient of discharge.
EquipementVenturi meter fitted in a horizontal pipe line with means of varying flow rate, U tube differential manometer.
Introduction and theory:The venturi meter meter are devices used for measurement of rate of flow of fluid through a pipe. The basis principle on which a venturi meter and orifice meter work is that by reducing the cross sectional area of flow passage, a pressure difference is created and the measurement of the pressure difference enables the determination of the discharge through the pipe. A venturi meter consists of (I) an inlet section followed by convergent cone (2) a cylindrical throat and (3) a gradually divergent cone. Since the cross sectional are of the throat is smaller than the cross sectional area of the inlet section, the velocity of flow
Orificemeter:An orifice meter is a cheap arrangement for measurement of discharge through pipes and its installation requires a smaller length as compared with venturi meter.
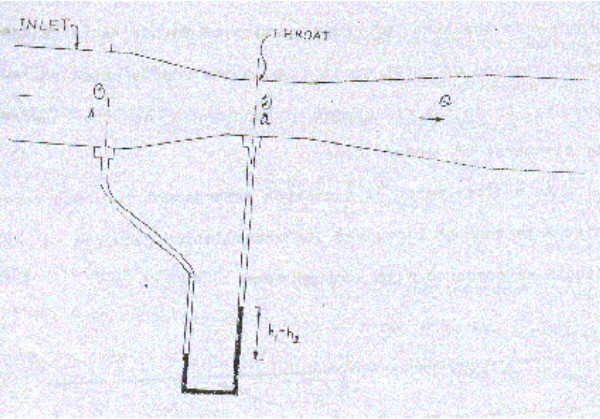
at the throat will become greater than that at the inlet section, according to continuity equation. The increase in the velocity of flow at the throat result in the decrease in the pressure at this section. A pressure difference is created between the inlet section and throat section which can be determined by 25 connecting a differential U-tube manometer between the pressure taps provided at these sections. The measurement of pressure difference between these sections enables the rate of flow of fluid (Q) to be calculated as
Q = Cda √2g Δh/√1-(-a/A)2
where a is the area of cross section of throat. A is the area of cross section of inlet section, g is the acceleration due to the gravity. Δh is the difference of head and Cd is the coefficient of discharge of venturi meter.
Experimental Set Up: The experimental set up consist of a circuit, through which the fluid is circulated continuously having a venturi meter, of 25mm dia and having d/D = .6. A regulating value is provided on the downstream side of the circuit to regulate the flow. The venturi meter is provided with two tapings one each at upstream and at the throat section.. A U tube differential manometer with common manifold is provided to measure the pressure difference between two sections. A collecting tank is used to find the actual discharge through the circuit.
Experimental procedure:Note down the relevant dimensions as diameter of pipeline, throat dia of venturimeter. Area of collecting tank, room temperature etc.
Pressure tapings of orifice meter are open, while of venturimeter (discussed in the next experiment) are closed.
The flow rate was adjusted to its maximum value.
By maintaining suitable amount of steady flow in the pipe circuit, there establishes a steady non uniform flow in the conduit. Time is allowed to stabilize the levels in the manometer tube.
The discharge flowing in the circuit is recorded together with the water level in left and right limbs of manometer tube. The flow rate is reduced in stages by means of flow control valve and the discharge and readings of manometer are recorded.
This procedure is repeated by closing the pressure tapings of for opening of venturimeter.
Observation and computation sheet.
Diameter of main pipe line D = 25mm
The ratio d/D = 0.6
Area of cross section of throat section, a = d = 15mm
Area of cross section of inlet section, A =
Area of collecting tank =
| Sr. No. | Discharge Measurement/Initial (cm)/Final(cm)/Time(s)Discharge, Q(cm3/s) | /Velocity, Q/A | Manometer Reading/Left Limb, h1(cm)/Right Limb, h2(cm)/Diff. of head in terms of water,Δh = 12.6(h1-h2) | Cd = Q√1-(a/A)2/a √2gh | Reynolds Number Re (DVrho/mu) |
Average C
Graph to plot :
Coment:





Get all latest content delivered to your email a few times a month.